Bayessche Schätzung von B-Spline-Kurven
| Betreuung: | Hamza Alkhatib, Johannes Bureick |
| Bearbeitung: | Daniel Golnik |
| Jahr: | 2016 |
| Laufzeit: | 2016 |
| Ist abgeschlossen: | ja |

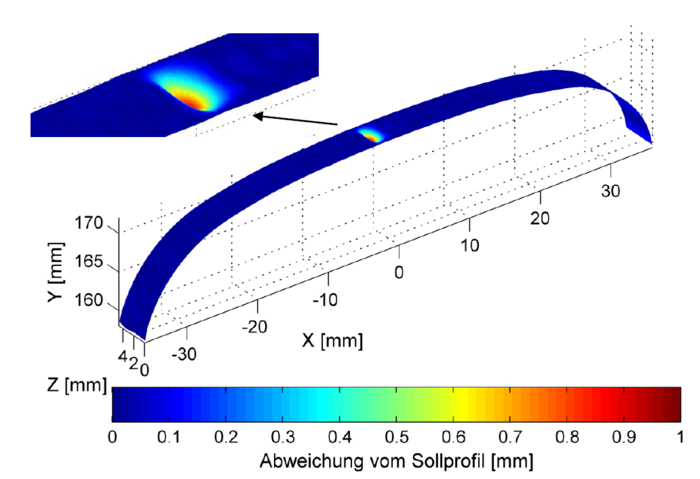
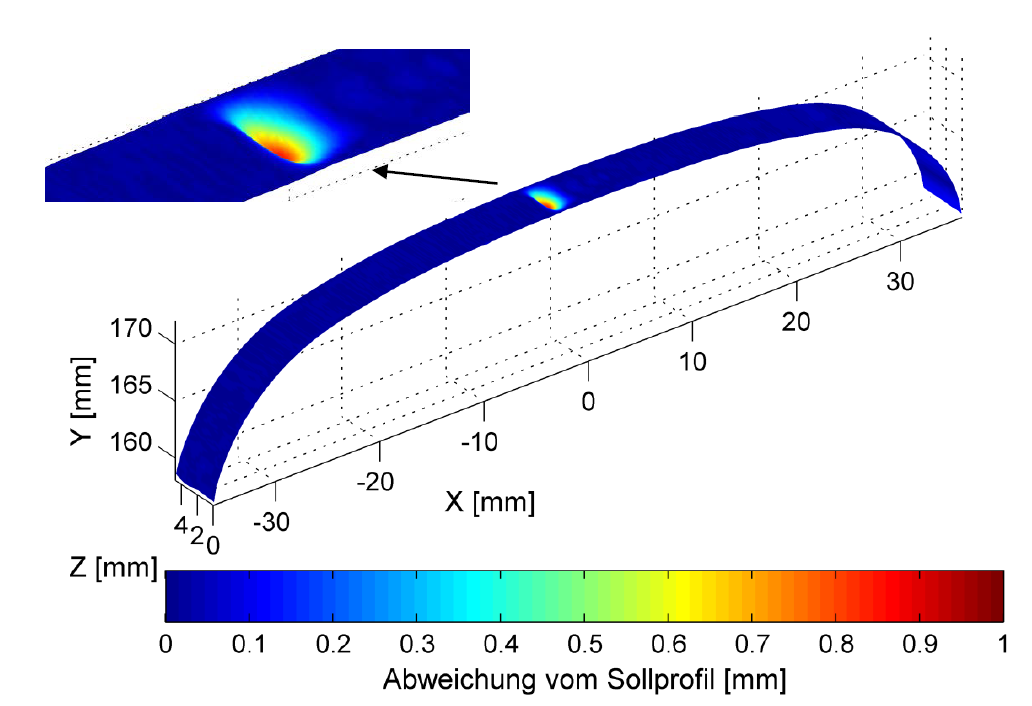
Frei-Form-Kurven und –Flächen, insbesondere B-Splines, sind optimal dazu geeignet, durch eine 3D-Punktwolke erfasste, komplexe Objekte zu approximieren.
Die optimale Bestimmung der B-Spline-Kurven und -Flächen umfasst die Schritte der Modellwahl, der Datenparametrisierung, der Knotenvektorbestimmung und der Kontrollpunktschätzung. Insbesondere hat die Bestimmung des Knotenvektors einen entscheidenden Einfluss auf die resultierende Güte der Approximation. Problematisch bei der Knotenvektorbestimmung ist, dass es keine analytische Funktion für die optimale Position der Knoten gibt und zudem viele lokale Optima der kleinste-Quadrate-Funktion auftreten. Aus diesem Grunde wurden verschiedene metaheuristische Verfahren entwickelt, mit der ein optimaler Knotenvektor bestimmt werden kann.
Herr Golnik hat im Rahmen seiner Arbeit ein kürzlich entwickeltes metaheuristische Verfahren für Kurven nach Bureick et al. (2016) aufgegriffen und durch Integration von Vorwissen (z.B. aus vorherigen Schätzungen oder Sollpunktwolken) erweitert und optimiert. Er hat untersucht welche Informationen in welcher Weise am sinnvollsten integriert werden können. Hierbei hat sich die Integration des Knotenvektors als vorteilhaft herausgestellt. In einem weiteren Schritt hat Herr Golnik das Verfahren nach Bureick et al. (2016), unter Verwendung der untersuchten Modifizierungen, auf die Approximation von B-Spline-Flächen erweitert.
Herr Golnik hat seine entwickelten Algorithmen auf verschiedene 3D-Punktwolken gescannter Schienen, welche sowohl Datenlücken als auch teilweise Schienendefekte enthielten, angewendet. Dadurch konnte Herr Golnik die Leistungsfähigkeit seiner Algorithmen evaluieren und weiter optimieren.






