Ableitung konsistenter Erdorientierungssparameter, Schwerfeldkoeffizienten zweites Grades und geophysikalische Anregungsfunktionen aus heterogener Daten
| Leitung: | Hansjörg Kutterer |
| Team: | Andrea Heiker |
| Jahr: | 2006 |
| Förderung: | DFG |
| Laufzeit: | 2006-2012 |
| Ist abgeschlossen: | ja |
Projektbeschreibung
Erdorientierungssparameter, Schwerfeldkoeffizienten und Anregungsfunktionen werden unabhängig von einander bestimmt. Sie beschreiben zum Teil redundant die Rotation und das Schwerefeld der Erde. Die heterogenen Daten müssen in ein einheitliches System integriert werden, um konsistente Zeitreihen ableiten zu können. Durch die Redundanz können Informationen über die Qualität der ursprünglichen Daten und Modelle gewonnen und die Inkonsistenzen quantifiziert werden.
Die Erdorientierungssparameter, die Schwerfeldkoeffizienten zweiten Grades und die Anregungsfunktionen werden mit Hilfe einer Ausgleichung nach der Methode der kleinsten Quadrate integriert. Die Integration der Daten wird durch folgende Probleme erschwert:
- Die Daten besitzen eine unterschiedliche zeitliche Auflösung
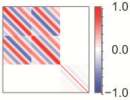
- Die Daten sind zum Teil hoch korreliert, ohne dass hinreichende Informationen über Korrelationen bekannt sind. Die Abbildung zeigt exemplarisch eine empirisch gewonnene Varianz-Kovarianzmatrix.
- Die funktionalen Bezeihungen sind nicht lineare Differenzialgleichungen, die in der Literatur durch lineare Differenzialgleichungen approximiert werden.
- Die Daten haben keinen einheitlichen Bezug, so dass aktuell nur relative Variationen jedoch keine absoluten Werte abgeleitet werden können.
Da die Daten eine unterschiedliche zeitlichen Auflösung besitzen und die funktionalen Beziehungen auf Differentialgleichungen beruhen, wurde das allgemein bekannte Gauß-Markov-Modell zu einem Gauß-Markov-Modell mit Nebenbedingungen erweitert, das auch eine Varianz-Kovarianz-Komponenten Schätzung umfasst. Mit der Varianz-Kovarianz-Komponenten Schätzung können unterschiedliche stochastische Modelle und deren Einfluss auf die Schätzung untersucht werden.
Sehr lange Zeitreihen können mit Hilfe des erweiterten Gauß-Markov-Modells aufgrund begrenzter Rechenressourcen kaum noch ausgewertet werden. Daher wird aktuell ein Kalman- bzw. ein Partikel / Bayesfilter entwickelt, um eine rekursive Auswertung der Zeitreihen zu ermöglichen.






